LeetCode_Longest Valid Parentheses

Posted on | In | Views:

Longest Valid Parentheses

Given a string containing just the characters ‘(‘ and ‘)’, find the length of the longest valid (well-formed) parentheses substring.
（最长有效括号对）

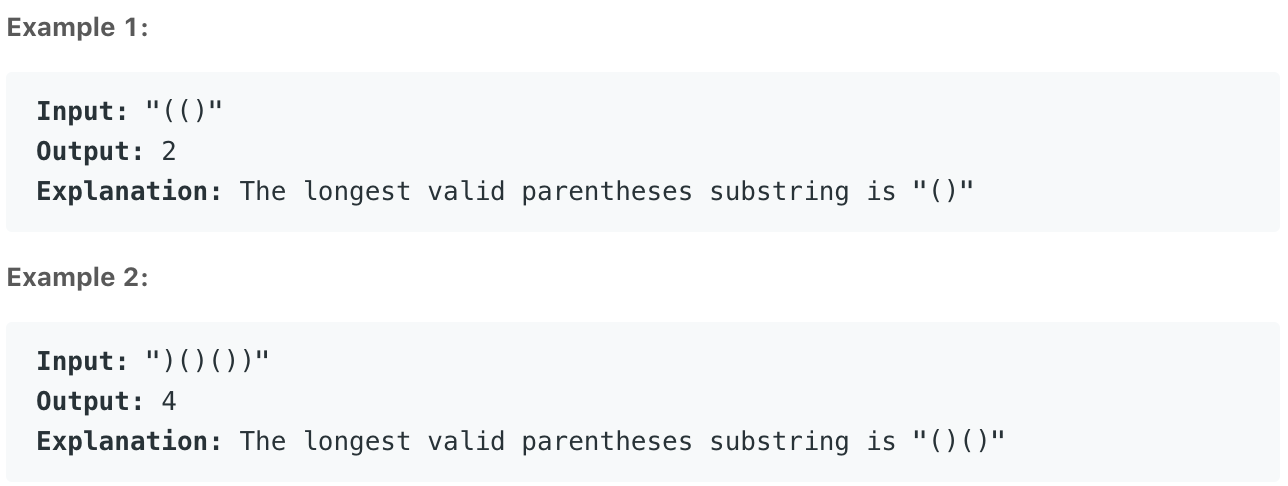
Example:



1.动态规划

这是一个很直观的动态规划的题目，需要分两种情况讨论：

  1. 当前字符为 ‘)’ 且前一个字符为 ‘(‘ ，则动态规划公式可以为 dp[i] = dp[i-2] + 2
  2. 当前字符为 ‘)’ 且前一个字符为 ‘)’ ，则我们需要考虑 s[i-dp[i-1]-1]，即上一个没有匹配成功的字符为 ‘(‘ 时，此时也算匹配成功，dp[i] = dp[i-1] + dp[i-dp[i-1]-2] + 2。 这里需要特别注意的是需要加上 dp[i-dp[i-1]-2]， 因为这也算是连续的匹配。
    具体实现过程如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution:
    def longestValidParentheses(self, s):
        """
        :type s: str
        :rtype: int
        """
        n = len(s)
        
        if n <= 1:
            return 0
        
        dp = [0 for _ in range(n)]
        
        for i in range(1, n):
            if s[i] == ')' and s[i-1] == '(':
                if i >=2:
                    dp[i] = dp[i-2] + 2
                else:
                    dp[i] = 2
            if s[i] == ')' and s[i-1] == ')':
                if i-dp[i-1]-1 >= 0 and s[i-dp[i-1]-1] == '(':
                    dp[i] = dp[i-1] + dp[i-dp[i-1]-2] + 2
        
        return max(dp)

2.栈

首先我们在栈顶 push 一个-1最为起始条件表示已经扫描的index，在遍历字符串的过程中，遇到 ‘(‘ 就 push 进去新的index，遇到 ‘)’ 就pop堆栈并分两种情况讨论：

  1. 此时堆栈为空，表示 ‘)’ 的个数大于 ‘(‘ ，因此我们可以把此时的 index push进去，表示重新开始；
  2. 此时堆栈不为空，表示前面有剩余，我们可以计算当前的 index 和栈顶的差表示最终匹配成功的个数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution:
    def longestValidParentheses(self, s):
        """
        :type s: str
        :rtype: int
        """
        n = len(s)
        
        stack = []
        stack.append(-1)
        
        max_re = 0
        for i, ch in enumerate(s):
            if ch == '(':
                stack.append(i)
            else:
                stack.pop()
                if len(stack) == 0:
                    stack.append(i)
                else:
                    max_re = max(max_re, i - stack[-1])
                    
        return max_re