LeetCode_Maximum Product Subarray

Posted on | In | Views:

Maximum Product Subarray

Given an integer array nums, find the contiguous subarray within an array (containing at least one number) which has the largest product.
（最大子串乘积）

Example:



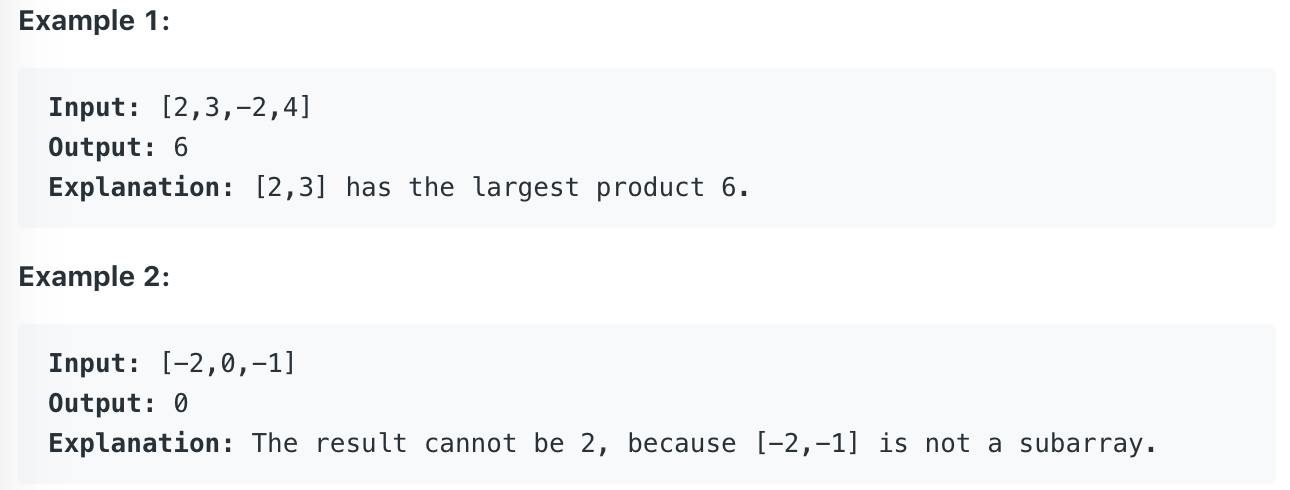
1. 动态规划

根据题意，需要找到数组中的某一个连续子数组，使得改部分的乘积最大，很明显的动规题目。具体实现过程如下：

Note: 其中需要特别注意的是数组中存在负数，因此需要在遍历过程中考虑乘积最小的部分，这样通过符号的翻转反而可以得到最大值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution:
    def maxProduct(self, nums: List[int]) -> int:
        if not nums:
            return 0
        n = len(nums)
        # 实际上可以不用维护一个数组，简单的变量即可。
        dp_max = [0 for _ in range(n)]
        dp_min = [0 for _ in range(n)]
        
        dp_max[0] = nums[0]
        dp_min[0] = nums[0]
        
        for i in range(1, n):
            if nums[i] >= 0:
                dp_max[i] = max(dp_max[i-1] * nums[i], nums[i])
                dp_min[i] = min(dp_min[i-1] * nums[i], nums[i])
            else:
                dp_max[i] = max(dp_min[i-1] * nums[i], nums[i])
                dp_min[i] = min(dp_max[i-1] * nums[i], nums[i])
        
        return max(dp_max)

降低空间复杂度的情况如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution:
    def maxProduct(self, nums: List[int]) -> int:
        if not nums:
            return 0
      
        dp_max, dp_min, result = nums[0], nums[0], nums[0]
        for i in range(1, len(nums)):
            temp1, temp2 = dp_min * nums[i],  dp_max * nums[i]
            dp_max = max(temp1, temp2, nums[i])
            dp_min = min(temp1, temp2, nums[i])
            result = max(dp_max, result)
            
        return result