LeetCode_Course Schedule

Posted on | In | Views:

Course Schedule

There are a total of n courses you have to take, labeled from 0 to n-1. Some courses may have prerequisites, for example to take course 0 you have to first take course 1, which is expressed as a pair: [0,1]. Given the total number of courses and a list of prerequisite pairs, is it possible for you to finish all courses?
（课程清单）

Example:



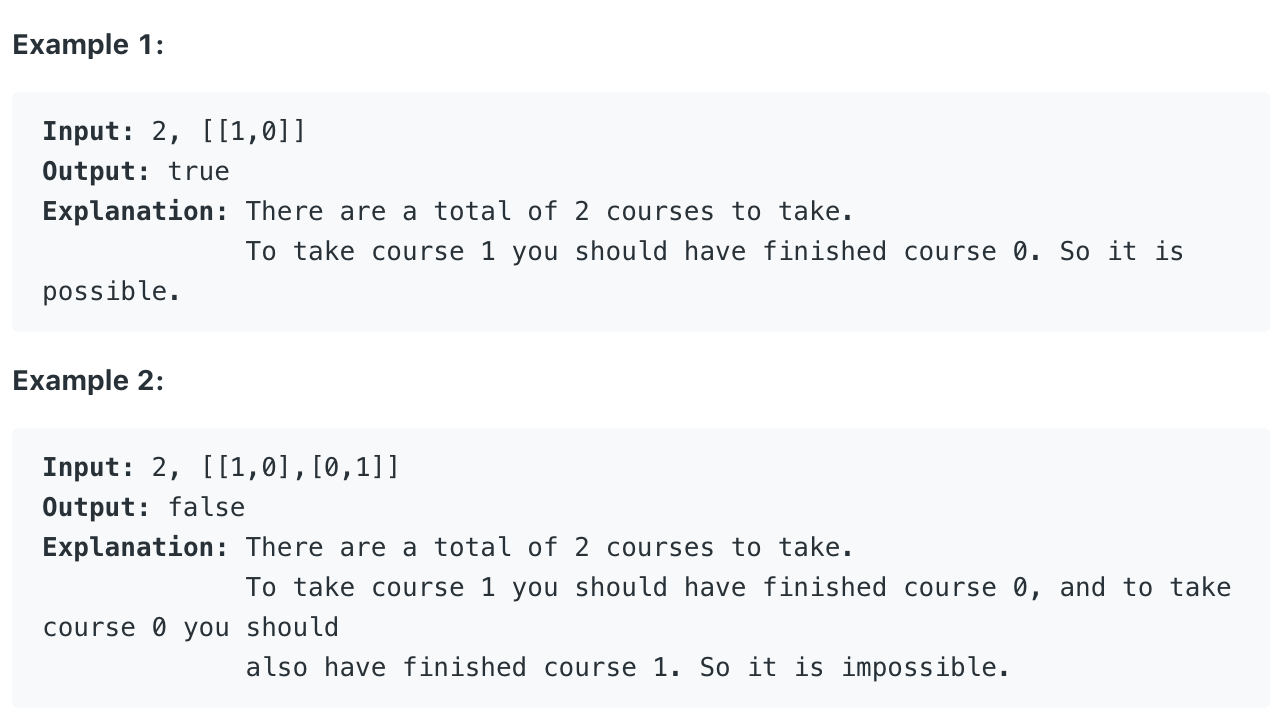
不同的课程可能存在前置课程，要求能否在不存在矛盾的情况下安排这些课程（如上述1必须在0的前面），这实质上是一个在有向图中判断是否存在圆环的过程，具体的课程安排则是一个拓扑排序的过程。

  1. 如果一个有向图的任意顶点都无法通过一些有向边回到自身，那么称这个有向图为有向无环图(Directed Acyclic Graph, DAG)。
  2. 拓扑排序是将有向无环图G的所有顶点排成一个线性序列，使得对图G中的任意两个顶点u、v，如果存在边u->v，那么在序列中u一定在v前面。这个序列又被称为拓扑序列。

1. 拓扑排序-BFS

这里我们需要用到一个图里入度的概念，在初始的图中，入度为0的点，即是课程中最基础的课程（需要先修），在找到图中所有入度为0的点以后，将它们依次放入一个队列中，每次循环从队列头提取一个点，然后将这个点放入图中查询，查出哪些点被这个点所指向，并依次将这些点的入度减1，直观上的看的话，即是一个删除一个入度为0的点的操作，每次减1时，检测其他节点的入度，若出现新的入度为0的点，将其加入队列，循环往复，直到队列为空为止。

循环结束后，再次检查每个节点的入度，若该图是拓扑有序的，则在循环操作中，所有的入度都会变为0。若不是拓扑有序的，则还会有入度不为0的点，即存在环。时间复杂度是O(N^2)，空间复杂度是O(N)。具体实现过程如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
import collections

class Solution:
    def canFinish(self, numCourses: int, prerequisites: List[List[int]]) -> bool:
        graph = collections.defaultdict(list)
        indegrees = collections.defaultdict(int)
        
        for u, v in prerequisites:
            graph[v].append(u)
            indegrees[u] += 1
        
        queue = [u for u in range(numCourses) if indegrees[u] == 0]
        
        if not queue:
            return False
        
        while queue:
            v = queue[0]
            for u in graph[v]:
                indegrees[u] -= 1
                if indegrees[u] == 0:
                    queue.append(u)
            queue.remove(v)
        
        for u in range(numCourses):
            if indegrees[u] != 0:
                return False
        
        return True

2. 拓扑排序-DFS

同样是拓扑排序，但是换了个做法，使用DFS。这个方法是，我们每次找到一个新的点，判断从这个点出发是否有环，具体做法是使用一个 visited 数组：

  1. 当 visited[i] 值为0，说明还没判断这个点；
  2. 当 visited[i] 值为1，说明当前的循环正在判断这个点；
  3. 当 visited[i] 值为2，说明已经判断过这个点，含义是从这个点往后的所有路径都没有环，认为这个点是安全的。

那么，我们对每个点出发都做这个判断，检查这个点出发的所有路径上是否有环，

  1. 如果判断过程中找到了当前的正在判断的路径（visited[i] == 1），说明有环；
  2. 如果找到了已经判断正常的点（visited[i] == 2），说明往后都不可能存在环，所以认为当前的节点也是安全的；
  3. 如果当前点是未知状态，那么先把当前点标记成正在访问状态visited[i] = 1），然后找后续的节点，直到找到安全的节点为止。最后如果到达了无路可走的状态，说明当前节点是安全的。

时间复杂度是O(N)，空间复杂度是O(N)。具体实现过程如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
import collections

class Solution:
    def dfs(self, graph, visited, i):
        if visited[i] == 1:
            return False
        if visited[i] == 2:
            return True

        visited[i] = 1
        for j in graph[i]:
            if not self.dfs(graph, visited, j):
                return False
        visited[i] = 2
        return True

    def canFinish(self, numCourses: int, prerequisites: List[List[int]]) -> bool:
        graph = collections.defaultdict(list)
      
        for u, v in prerequisites:
            graph[v].append(u)
        
        visited = [0] * numCourses
        
        for i in range(numCourses):
            if not self.dfs(graph, visited, i):
                return False
        return True